다이나믹 프로그램은
메모리 공간을 약간 더 사용하여 연산 속도를 비약적으로 증가시키는 방법이다.
다음의 2가지 조건을 만족할 때 다이나믹 프로그래밍을 사용할 수 있다.
- 큰 문제를 작은 문제로 나눌 수 있음
- 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일함
위 조건을 만족하는 대표적인 예로 피보나치 수열이 있다. 피보나치 수열은 다음의 점화식을 만족하는 수열이다.
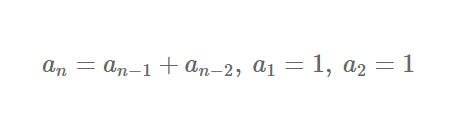
해당 피보나치 수열을 Python 재귀함수로 구현한다면 다음과 같은 코드로 표현할 수 있다.
import time
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(x-1) + fibo(x-2)
for num in range(5, 40, 10):
start = time.time()
res = fibo(num)
print(res, '-> 러닝타임:', round(time.time() - start(), 2), '초')위와 같은 단순 재귀함수로 구현할 경우 x 값이 커짐에 따라 연산 수행시간이 급격하게 늘어남을 알 수 있다.

이러한 문제를 해결하기 위해 DP를 사용해야 한다.
Dynamic Programming의 핵심은 바로 한번에 결과를 수행한 것을 메모리에 저장해 놓고 다음에 똑같은 결과가 필요하면 그 때 다시 연산하지 않고 메모리에 저장된 값을 가져와 쓰는 것이다.
이러한 것을 메모제이션(캐싱) 기법이라고도 한다.
다음은 재귀함수를 사용한 DP로 피보나치 수열을 구현한 코드이다.
import time
d = [0] * 50
def fibo(x):
if x == 1 or x == 2:
return 1
if d[x] != 0:
return d[x]
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
for num in range(5, 40, 10):
start = time.time()
res = fibo(num)
print(res, '-> 러닝타임:', round(time.time() - start, 2), '초')위의 코드로 x 값이 늘어남에 따라 변하는 함수 러닝타임은 다음과 같다.

단순 재귀함수로 구현한 것과 다르게 x 값이 증가해도 함수 러닝 타임이 기하급수적으로 증가하지 않는 것을 볼 수 있다.
이렇게 재귀함수를 사용해 구현하는 다이나믹 프로그래밍 방법은 메모제이션 기법 Top - Down 방식이라고 한다.
즉, 큰 문제를 해결하기 위해 작은 문제를 호출하는 것이다.
반면 재귀함수를 사용하지 않고 단순 반복문을 사용해 DP를 구현할 수 있다.
d = [0] * 100
d[1] = 1
d[2] = 1
N = 99
for i in range(3, N+1):
d[i] = d[i-1] + d[i-2]
print(d[N])위와 같은 방식은 작은 문제부터 답을 도출해나가는 Bottom - Up 방식이라고 부른다.
Top - Down 방식에서는 이미 수행한 결과를 저장하는 것을 메모제이션,
Bottom - Up 방식에서는 DP 테이블이라고 말한다.
Top - Down 방식의 메모제이션 기법은 사전(dictionary) 자료형을 이용할 수 있는데, 이는 수열처럼 연속적이지 않은 자료가 주어질 때 유용하다. 즉 An을 계산하기 위해 A0 부터 An-1 모두를 살펴보는 것이 아닌 일부 결과만 필요한 경우이다.
특별한 상황이 아니라면 단순 반복문을 활용하는 Bottom - Up 방식의 DP 방법을 권장한다.
만약 재귀함수를 사용하는 Top - Down 방식을 사용하다보면 재귀 횟수 제한 오류에 걸릴 수 있기 때문이다.
물론 이러한 오류가 나타났을 때 sys 라이브러리의 setrecursionlimit() 메서드를 호출해
재귀 제한 횟수를 늘려줄 수 있다.
참조 : [Python] Dynamic Programming(동적계획법) 알고리즘 (tistory.com)
[Python] Dynamic Programming(동적계획법) 알고리즘
🔊 이번 포스팅에는 최근에 Python으로 알고리즘을 공부하기 시작하면서 알게 된 여러 알고리즘의 원리와 Python으로 구현하는 방법에 대해 소개해보려 한다. 필자는 최근 알고리즘 공부를 '나동
techblog-history-younghunjo1.tistory.com
다이나믹 프로그램은
메모리 공간을 약간 더 사용하여 연산 속도를 비약적으로 증가시키는 방법이다.
다음의 2가지 조건을 만족할 때 다이나믹 프로그래밍을 사용할 수 있다.
- 큰 문제를 작은 문제로 나눌 수 있음
- 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일함
위 조건을 만족하는 대표적인 예로 피보나치 수열이 있다. 피보나치 수열은 다음의 점화식을 만족하는 수열이다.
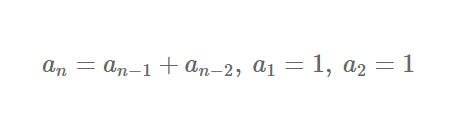
해당 피보나치 수열을 Python 재귀함수로 구현한다면 다음과 같은 코드로 표현할 수 있다.
import time def fibo(x): if x == 1 or x == 2: return 1 return fibo(x-1) + fibo(x-2) for num in range(5, 40, 10): start = time.time() res = fibo(num) print(res, '-> 러닝타임:', round(time.time() - start(), 2), '초')
위와 같은 단순 재귀함수로 구현할 경우 x 값이 커짐에 따라 연산 수행시간이 급격하게 늘어남을 알 수 있다.

이러한 문제를 해결하기 위해 DP를 사용해야 한다.
Dynamic Programming의 핵심은 바로 한번에 결과를 수행한 것을 메모리에 저장해 놓고 다음에 똑같은 결과가 필요하면 그 때 다시 연산하지 않고 메모리에 저장된 값을 가져와 쓰는 것이다.
이러한 것을 메모제이션(캐싱) 기법이라고도 한다.
다음은 재귀함수를 사용한 DP로 피보나치 수열을 구현한 코드이다.
import time d = [0] * 50 def fibo(x): if x == 1 or x == 2: return 1 if d[x] != 0: return d[x] d[x] = fibo(x-1) + fibo(x-2) return d[x] for num in range(5, 40, 10): start = time.time() res = fibo(num) print(res, '-> 러닝타임:', round(time.time() - start, 2), '초')
위의 코드로 x 값이 늘어남에 따라 변하는 함수 러닝타임은 다음과 같다.

단순 재귀함수로 구현한 것과 다르게 x 값이 증가해도 함수 러닝 타임이 기하급수적으로 증가하지 않는 것을 볼 수 있다.
이렇게 재귀함수를 사용해 구현하는 다이나믹 프로그래밍 방법은 메모제이션 기법 Top - Down 방식이라고 한다.
즉, 큰 문제를 해결하기 위해 작은 문제를 호출하는 것이다.
반면 재귀함수를 사용하지 않고 단순 반복문을 사용해 DP를 구현할 수 있다.
d = [0] * 100 d[1] = 1 d[2] = 1 N = 99 for i in range(3, N+1): d[i] = d[i-1] + d[i-2] print(d[N])
위와 같은 방식은 작은 문제부터 답을 도출해나가는 Bottom - Up 방식이라고 부른다.
Top - Down 방식에서는 이미 수행한 결과를 저장하는 것을 메모제이션,
Bottom - Up 방식에서는 DP 테이블이라고 말한다.
Top - Down 방식의 메모제이션 기법은 사전(dictionary) 자료형을 이용할 수 있는데, 이는 수열처럼 연속적이지 않은 자료가 주어질 때 유용하다. 즉 An을 계산하기 위해 A0 부터 An-1 모두를 살펴보는 것이 아닌 일부 결과만 필요한 경우이다.
특별한 상황이 아니라면 단순 반복문을 활용하는 Bottom - Up 방식의 DP 방법을 권장한다.
만약 재귀함수를 사용하는 Top - Down 방식을 사용하다보면 재귀 횟수 제한 오류에 걸릴 수 있기 때문이다.
물론 이러한 오류가 나타났을 때 sys 라이브러리의 setrecursionlimit() 메서드를 호출해
재귀 제한 횟수를 늘려줄 수 있다.
참조 : [Python] Dynamic Programming(동적계획법) 알고리즘 (tistory.com)
[Python] Dynamic Programming(동적계획법) 알고리즘
🔊 이번 포스팅에는 최근에 Python으로 알고리즘을 공부하기 시작하면서 알게 된 여러 알고리즘의 원리와 Python으로 구현하는 방법에 대해 소개해보려 한다. 필자는 최근 알고리즘 공부를 '나동
techblog-history-younghunjo1.tistory.com