분할 정복이란
주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 계산하고
이를 병합해 문제를 해결하는 기법이다.
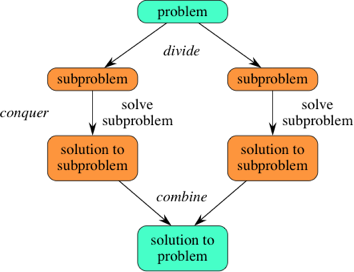
문제를 즉각 해결할 수 있을 때까지 재귀적으로 둘 이상의 하위 문제들로 나누고(Divide)
문제를 해결한 다음(Conquer) 그 결과를 이용해 다시 전체 문제를 해결하며 합치는 방법이다.
관련 알고리즘
분할 정복 방식으로 해결되는 문제로 다음 알고리즘이 있습니다.
- 정렬 문제(퀵 정렬, 병합 정렬)
- 큰 숫자 곱하기(Karatsuba 알고리즘) : n자리 수 2개를 곱하여 결과를 나타내는 알고리즘
- 이진 탐색 (Binary Search)
- Closet Pair of Points 문제 : 모든 point 쌍의 거리 중 최소의 거리를 찾는 문제
- Strassens's 알고리즘 : 두 행렬을 곱하는 효과적인 알고리즘
- Cooley-Turkey Fast Fourier Transform (FFT) 고속 푸리에 변환 알고리즘
알고리즘 설계
- 분할(Divide) : 주어진 문제를 같은 형태의 작은 문제로 나눈다.
- 정복(Conquer) : 충분히 나누어져 해결 가능한 작은 문제를 재귀적으로 해결한다.
- 통합(Combine) : 작은 문제에서 구한 해답을 서로 합쳐 본래의 문제에 대한 해답을 도출한다.
문제를 제대로 나누면 Conquer하는 건 쉽기 때문에 Divide를 제대로 하는 것이 가장 중요합니다.
주로 재귀 알고리즘이 많이 사용되는데, 이는 분할 정복 알고리즘 효율성을 깎아내릴 수 있습니다.
분할 정복 응용
병합 정렬 (Merge Sort)

- 정렬할 데이터 집합 크기가 0 또는 1이면 이미 정렬된 것으로 본다.
- 그렇지 않으면 리스트를 두 개의 균등한 크기로 분할한다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
(단, 병합할 때 데이터 집합의 원소는 순서에 맞춰 정렬한다.) - 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
이진 검색 (Binary Search)
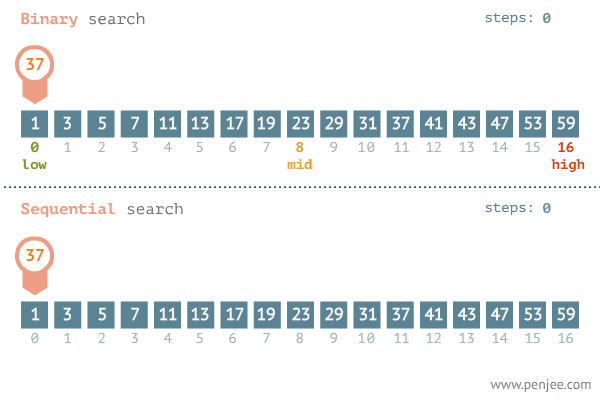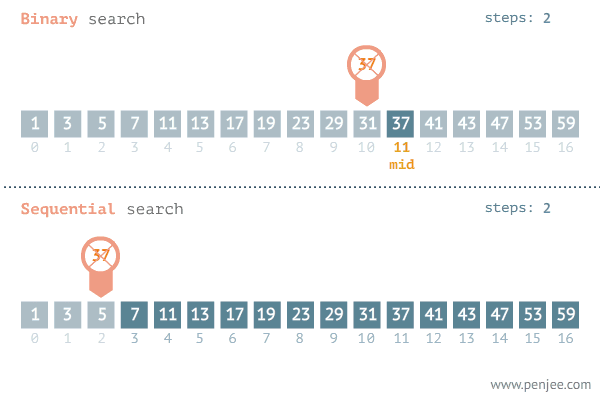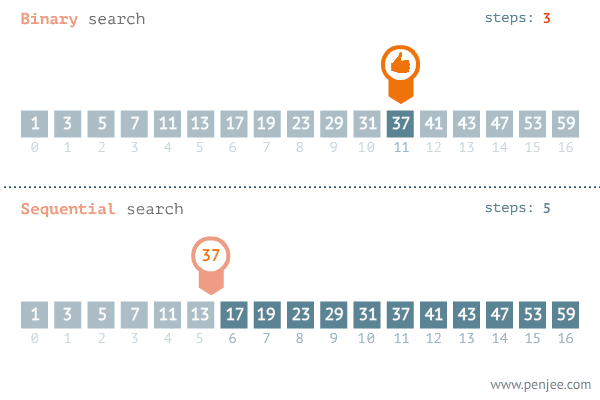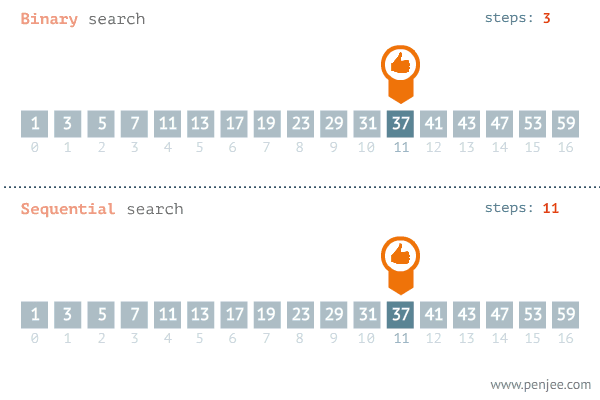
- 배열을 절반으로 나누는 과정을 수행한다.
- 찾으려는 값이 절반 중 하나의 위치에 있는지 확인한다.
- 배열을 절반으로 나누고, 찾으려는 값이 절반 중 하나에 위치에 있는지 확인한다.
시간 복잡도
- 비교 횟수 : log2n
레코드의 개수 n이 2의 거듭제곱이라고 가정하였을 때, n = 2^k 라고 표현할 수 있다.
ex) n = 2^3일 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 순환 호출 길이가 3이다.
이를 일반화하면 n = 2^k는 호출 깊이는 k 이다.
이 때, k = log2n이므로 비교 횟수는 log2n 이다. - 각 순환 호출 단계의 비교 연산 : n
각 순환 호출에서 전체 리스트의 거의 모든 레코드를 비교해야 하므로 n번의 비교가 발생한다.
따라서 시간 복잡도는 순환 호출 깊이 * 각 순환 호출 단계 비교 연산 = nlong2n 가 된다.
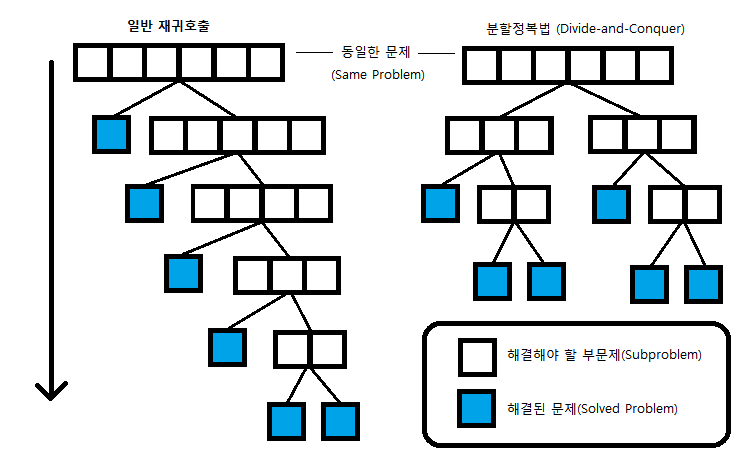
분할 정복의 재귀적 방법에 대한 비교
💡 분할 정복의 경우 분할 -> 정복 -> 통합 과정으로 해결해 나가기에
해결 과정이 '분할'하는 과정과 '해결'하는 과정으로 분리되어 있습니다.
그리고 별도의 메모리 사용 없이 문제를 작은 부분으로 나누어 해결하여 속도가 상대적으로 빠릅니다.
| 분류 | 분할 정복 알고리즘 | 재귀 함수 |
| 정의 | 문제를 작은 부분으로 나누어 해결하는 방법 |
함수 내부에서 자기 자신을 호출하여 문제를 해결하는 방법 |
| 해결 과정 차이 | 문제를 '분할', '해결'하는 과정으로 분리됨 |
자기 자신을 호출하여 문제를 해결하는 과정이 하나의 과정으로 이루어짐 |
| 속도 차이 | 일반적으로 더 빠른 속도로 동작 | 호출 스택 등 추가적 메모리가 사용되어 속도가 느려질 수 있음 |
| 대규모 문제에 대한 차이 | 대규모 문제 해결에 용이함 | 호출 스택 한계로 대규모 문제 해결 어려움 |
참조 : https://gamedevlog.tistory.com/58
분할 정복(Divide and Conquer)
Goal 분할 정복에 대해 설명할 수 있다. 분할 정복 한 문제를 둘 이상의 부분 문제(sub-problem)로 나누어 해결하고 이를 합쳐 원래 문제를 해결하는 기법 분할 정복 알고리즘은 다음과 같이 세 부분
gamedevlog.tistory.com
분할 정복이란
주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 계산하고
이를 병합해 문제를 해결하는 기법이다.

문제를 즉각 해결할 수 있을 때까지 재귀적으로 둘 이상의 하위 문제들로 나누고(Divide)
문제를 해결한 다음(Conquer) 그 결과를 이용해 다시 전체 문제를 해결하며 합치는 방법이다.
관련 알고리즘
분할 정복 방식으로 해결되는 문제로 다음 알고리즘이 있습니다.
- 정렬 문제(퀵 정렬, 병합 정렬)
- 큰 숫자 곱하기(Karatsuba 알고리즘) : n자리 수 2개를 곱하여 결과를 나타내는 알고리즘
- 이진 탐색 (Binary Search)
- Closet Pair of Points 문제 : 모든 point 쌍의 거리 중 최소의 거리를 찾는 문제
- Strassens's 알고리즘 : 두 행렬을 곱하는 효과적인 알고리즘
- Cooley-Turkey Fast Fourier Transform (FFT) 고속 푸리에 변환 알고리즘
알고리즘 설계
- 분할(Divide) : 주어진 문제를 같은 형태의 작은 문제로 나눈다.
- 정복(Conquer) : 충분히 나누어져 해결 가능한 작은 문제를 재귀적으로 해결한다.
- 통합(Combine) : 작은 문제에서 구한 해답을 서로 합쳐 본래의 문제에 대한 해답을 도출한다.
문제를 제대로 나누면 Conquer하는 건 쉽기 때문에 Divide를 제대로 하는 것이 가장 중요합니다.
주로 재귀 알고리즘이 많이 사용되는데, 이는 분할 정복 알고리즘 효율성을 깎아내릴 수 있습니다.
분할 정복 응용
병합 정렬 (Merge Sort)

- 정렬할 데이터 집합 크기가 0 또는 1이면 이미 정렬된 것으로 본다.
- 그렇지 않으면 리스트를 두 개의 균등한 크기로 분할한다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
(단, 병합할 때 데이터 집합의 원소는 순서에 맞춰 정렬한다.) - 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
이진 검색 (Binary Search)

- 배열을 절반으로 나누는 과정을 수행한다.
- 찾으려는 값이 절반 중 하나의 위치에 있는지 확인한다.
- 배열을 절반으로 나누고, 찾으려는 값이 절반 중 하나에 위치에 있는지 확인한다.
시간 복잡도
- 비교 횟수 : log2n
레코드의 개수 n이 2의 거듭제곱이라고 가정하였을 때, n = 2^k 라고 표현할 수 있다.
ex) n = 2^3일 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 순환 호출 길이가 3이다.
이를 일반화하면 n = 2^k는 호출 깊이는 k 이다.
이 때, k = log2n이므로 비교 횟수는 log2n 이다. - 각 순환 호출 단계의 비교 연산 : n
각 순환 호출에서 전체 리스트의 거의 모든 레코드를 비교해야 하므로 n번의 비교가 발생한다.
따라서 시간 복잡도는 순환 호출 깊이 * 각 순환 호출 단계 비교 연산 = nlong2n 가 된다.
분할 정복의 재귀적 방법에 대한 비교
💡 분할 정복의 경우 분할 -> 정복 -> 통합 과정으로 해결해 나가기에
해결 과정이 '분할'하는 과정과 '해결'하는 과정으로 분리되어 있습니다.
그리고 별도의 메모리 사용 없이 문제를 작은 부분으로 나누어 해결하여 속도가 상대적으로 빠릅니다.
| 분류 | 분할 정복 알고리즘 | 재귀 함수 |
| 정의 | 문제를 작은 부분으로 나누어 해결하는 방법 |
함수 내부에서 자기 자신을 호출하여 문제를 해결하는 방법 |
| 해결 과정 차이 | 문제를 '분할', '해결'하는 과정으로 분리됨 |
자기 자신을 호출하여 문제를 해결하는 과정이 하나의 과정으로 이루어짐 |
| 속도 차이 | 일반적으로 더 빠른 속도로 동작 | 호출 스택 등 추가적 메모리가 사용되어 속도가 느려질 수 있음 |
| 대규모 문제에 대한 차이 | 대규모 문제 해결에 용이함 | 호출 스택 한계로 대규모 문제 해결 어려움 |

참조 : https://gamedevlog.tistory.com/58
분할 정복(Divide and Conquer)
Goal 분할 정복에 대해 설명할 수 있다. 분할 정복 한 문제를 둘 이상의 부분 문제(sub-problem)로 나누어 해결하고 이를 합쳐 원래 문제를 해결하는 기법 분할 정복 알고리즘은 다음과 같이 세 부분
gamedevlog.tistory.com