💡 오늘의 학습 키워드
- 두 개 뽑아서 더하기
- 타겟 넘버
두 개 뽑아서 더하기
문제 링크 : https://school.programmers.co.kr/learn/courses/30/lessons/68644
문제 설명
정수 배열 numbers가 주어집니다.
numbers에서 서로 다른 인덱스에 있는 두 개의 수를 뽑아 더해서 만들 수 있는
모든 수를 배열에 오름차순으로 담아 return 하도록 solution 함수를 완성해주세요.
제한 사항
1. numbers의 길이는 2 이상 100 이하입니다.
2. numbers의 모든 수는 0 이상 100 이하입니다.
문제 회고
💡 어떤 문제가 있었고, 나는 어떤 시도를 했는지 그리고 새롭게 안 사실은 무엇인지
특정 값을 뽑아서 경우의 수를 구하는 문제로 순열이나 조합을 사용해야 하는 문제였습니다.
c++과 다르게 itertool 라이브러리에서 간편하게 combinations 함수를 사용할 수 있었습니다.
제가 생각한 문제 해결 방법은 크게 다음과 같습니다.
- 입력 값을 조합으로 2개를 뽑는 경우의 수를 저장합니다.
- 저장된 각각의 원소를 sum 함수로 더한 후 answer 리스트에 삽입합니다.
- 만약 answer 리스트에 존재하는 값일 경우를 제외하여 중복을 방지합니다.
- 저장된 리스트를 오름차순으로 정렬합니다.
처음 풀이는 combinations 함수 결과 값을 리스트로 저장하고,
반복문을 순회하며 리스트 원소의 중복을 제거했습니다.
그리고 answer.sort()를 따로 구현한 후 결과 값을 리턴하는 형태였습니다.
사실 combinations 함수의 반환 값을 정확하게 확인하지 못해 리스트로 반환해야 한다는 생각으로
combination 결과 값 저장을 따로 하게 되었는데,
combinations 함수의 반환 값을 확인 해보니 튜플로 반환된다는 사실을 알았습니다.
그리고 sorted 함수 결과 값을 리스트로 반환하면 해당 작업을 줄일 수 있을 거라 생각했습니다.
그렇게 코드를 다시 보니 set 자료구조가 떠올랐습니다. 이렇게 추가 조건문 없이 중복된 값을 제거해 주니,
한 줄만으로 간결하게 문제를 해결할 수 있었습니다. 풀이 순서를 다시 정리하면 다음과 같습니다.
- combinations(numbers, 2) 를 사용해 모든 2개의 숫자 조합을 생성합니다.
- 각 조합의 합을 계산합니다.
- 중복된 합을 제거하기 위해 set 함수를 사용합니다.
- sorted 함수를 통해 새롭게 리스트를 생성하여 결과를 정렬해줍니다.
마지막으로 이렇게 복잡한 for 루프 없이 간결하게 풀이해보았습니다.
💡 내가 해결한 방식은?
반복문을 통한 중복 제거 (풀이 시간 : 10분)
from itertools import combinations
def solution(numbers):
answer = []
# 조합으로 2개를 뽑는 경우의 수 저장
num = list(combinations(numbers, 2))
# 중복된 수 제거
for ans in num:
if sum(ans) in answer:
continue
answer.append(sum(ans))
return sorted(answer)
set 자료구조를 통한 중복 제거 (풀이 시간 : 15분)
from itertools import combinations
def solution(numbers):
return sorted(set(sum(pair) for pair in combinations(numbers, 2)))
타겟 넘버
문제 링크 : https://school.programmers.co.kr/learn/courses/30/lessons/43165?language=python3
문제 설명
n개의 음이 아닌 정수들이 있습니다.
이 정수들을 순서를 바꾸지 않고 적절히 더하거나 빼서 타겟 넘버를 만들려고 합니다.
예를 들어 [1, 1, 1, 1, 1]로 숫자 3을 만들려면 다음 다섯 방법을 쓸 수 있습니다.
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
사용할 수 있는 숫자가 담긴 배열 numbers, 타겟 넘버 target이 매개변수로 주어질 때
숫자를 적절히 더하고 빼서 타겟 넘버를 만드는 방법의 수를 return 하도록 solution 함수를 작성해주세요.
제한 사항
1. 주어지는 숫자의 개수는 2개 이상 20개 이하입니다.
2. 각 숫자는 1 이상 50 이하인 자연수입니다.
3. 타겟 넘버는 1 이상 1000 이하인 자연수입니다.
문제 회고
💡 어떤 문제가 있었고, 나는 어떤 시도를 했는지 그리고 새롭게 안 사실은 무엇인지
문제 자체는 DFS 방식을 사용해 2가지 경우의 재귀 접근을 통해 해결하였습니다.
dfs 함수의 파라미터는 (인덱스, 연산 결과) 형태로 인덱스가 증가할 때마다 연산 결과를
재귀적으로 저장하도록 구성했습니다.
함수 상단 기저 조건 세팅에 변수 설정에서 약간의 고민이 있었습니다.
solution 함수에서한 answer 변수를 사용해야 하는데, dfs 함수에 따로 변수를 생성하자니
다른 방법이 있을 것 같았습니다. (c++에서는 그냥 전역변수로 사용했었는데..)
결국 파이썬의 전역 / 로컬 변수 설정을 어떻게 하는지 구글링 해 보았고,
global, nonlocal 키워드에 대하여 학습한 후 nonlocal 키워드를 사용하게 되었습니다.
nonlocal 키워드로 answer 변수에 값을 저장하도록 하여 기저 조건 세팅을 완료할 수 있었습니다.
이후 연산 결과 값을 인덱스가 증가할 때마다 기존 연산 결과 값에
해당 인덱스의 numbers 배열 값을 더해주는 재귀 코드와 빼주는 재귀 코드 2줄을 추가해주었습니다.
DFS 풀이를 마치고 다른 스터디 멤버가 BFS 풀이와 시간복잡도 관한 글을 올려 BFS 방식으로도 풀어보았습니다.
기저조건과 재귀 함수 세팅은 DFS와 큰 차이가 없어 큐와 스택을 넣어보며 시간 복잡도를 비교해보았는데,
특정 TC에서 BFS가 DFS에 비해 속도가 느린 것을 확인할 수 있었습니다.
DFS에서 재귀함수로 함수를 호출하는게 BFS에서 큐, 스택을 통해 처리하는 것보다 빨라서라고 생각이 들었는데,
다른 스터디 멤버분은 BFS에서 deque 사용을 하게 될 때의 메모리 문제일 것이라고 생각하셨습니다.
시간 복잡도 관련해서 제가 작성한 코드의 속도와 함께 아래에 글로 기록해두었습니다.
DFS

BFS + Stack
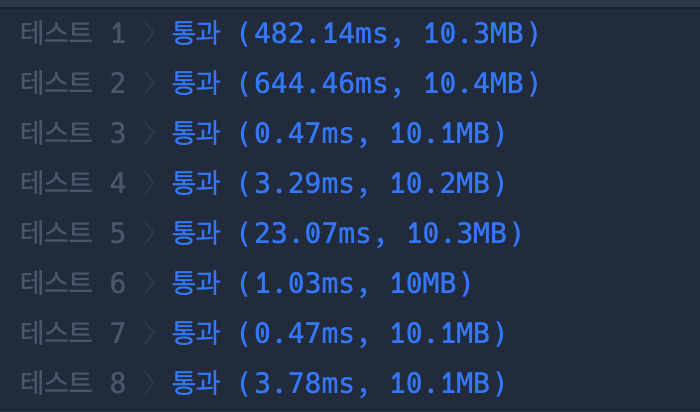
BFS + Queue

파이썬의 deque는 doubly-linked list 자료구조로 구현되어 있습니다.
이 자료구조는 양쪽 끝에서 삽입과 삭제 연산이 O(1)의 시간복잡도를 가지는 장점이 있습니다.
하지만 deque의 내부 구현에는 오버헤드가 있습니다.
각 노드가 이전 노드와 다음 노드를 가리키는 포인터를 가지고 있어야 하므로
메모리 사용량이 리스트보다 크고, 노드 간 링크 정보를 유지하기 위한 추가 작업이 필요합니다.
반면 DFS는 재귀 호출 또는 스택을 사용하므로 오버헤드가 작습니다.
단순히 방문 여부 배열만 유지하면 되기 때문입니다. 그래서 문제에 따라 다르겠지만,
일반적으로 DFS가 BFS보다 빠른 경향이 있습니다. 다만 BFS는 최단 경로를 보장하는 장점이 있습니다.
따라서 문제의 특성에 따라 적절한 방식을 선택해야 합니다.
요약하면, deque의 구현 오버헤드 때문에 BFS가 DFS보다 더 느린 결과가 나왔을 것으로 추측됩니다.
하지만 실제로는 구체적인 문제 상황과 입력 데이터에 따라 달라질 수 있습니다.
💡 내가 해결한 방식은?
DFS
def solution(numbers, target):
answer = 0
def dfs(index, value):
if index == len(numbers):
# dfs 통해 타겟 넘버에 접근했을 때 +1
if value == target:
nonlocal answer
answer += 1
return
# 재귀를 통해 index를 순회하며 +,- 연산을 누적 합니다.
dfs(index+1, value+numbers[index])
dfs(index+1, value-numbers[index])
dfs(0, 0)
return answer
BFS + Queue
def solution(numbers, target):
answer = 0
queue = [(0, 0)]
while queue:
index, sum = queue.pop()
if index == len(numbers):
if sum == target:
answer += 1
continue
queue.append((index + 1, sum + numbers[index]))
queue.append((index + 1, sum - numbers[index]))
return answer
BFS + Stack
def solution(numbers, target):
answer = 0
stack = [(0, 0)]
while stack:
index, sum = stack.pop()
if index == len(numbers):
if sum == target:
answer += 1
continue
stack.append((index + 1, sum + numbers[index]))
stack.append((index + 1, sum - numbers[index]))
return answer
TIL
확실히 c++에서 제한 조건에 맞게 배열 크기까지 직접 세팅해주는 것과 다르게
파이썬은 크기 고민이 상대적(?)으로 적다는 느낌을 받았다. 복잡한 문제에서는 다를 수 있겠지만,,
첫 번째 문제에서는 어떤 함수를 사용하더라도 반환 값이 정확히 어떻게 되는지 알아야
효율적인 코드 작성이 된다는 점을 체득할 수 있었다.
또 이 문제에서는 itertools 라이브러리의 조합, 순열 함수를 사용하여 풀이했는데,
나중에 어떻게 커스터마이징 해야할 지 모르니 따로 직접 구현하는 코드도 한번 만들어보아야 겠다.
두 번째 문제에서는 목차 상단에 DFS, BFS 라고 적혀 있어 접근 방식을 미리 안 상태로 문제를 접근해버렸다..
파이썬으로는 DFS, BFS 풀이가 처음이라 결국 구글링을 통해 예시 코드를 보아야 된다(?)고 합리화 하며
문제 풀이를 시작했고, 이왕 공부하는 겸 BFS, DFS 두 가지 방식으로 모두 풀어보며 시간복잡도까지 확인해보았다.
nonlocal을 사용했는데, 뭔가 c++에서 전역변수로 던져놓고 푸는 방식이 더 편했던거 같기도 하고..
그럼에도 확실히 DFS, BFS 구현은 c++보다 파이썬이 간결하고 가독성이 좋다..
이 부분은 나중에 map 을 통한 DFS 완전 탐색 문제도 한번 풀어봐야 겠다.